The Dirty Little Secrets of NURBS
Stephen M.
Hollister, New Wave Systems, Inc.
Copyright
2001, All Rights Reserved
www.pilot3d.com
Introduction
There is nothing more flexible than a piece of paper, a pencil, and the human brain. Once you begin using a computer for shape design, you are forced into the limitations and idiosyncrasies of the program and its underlying mathematical geometry technique. In exchange, however, you get the following and more.
·
Automatic matching of geometry in all views
·
Automatic 2D view and section drawings
·
Simple correction and modification of the design
·
Accurate full-size templates/patterns
·
Surface and volume calculations
·
3D Rendering
Many feel that because of these benefits and capabilities,
there are few or no complications or difficulties in designing by
computer. This could be blamed on
something I call "the rendering effect." One look at a 3D rendered geometric model with all of the colors,
shading, and all of the details defined in 3D, and it is hard to imagine anything
a computer can't do. When I look at a
picture like that, I think of the following:
·
Is the geometry accurate enough for construction use?
·
How long did it take to model the geometry? (Rendering is
easy, modeling is difficult.)
·
Is the geometry smooth and fair?
Renderings may look good in a brochure, but the 3D model
used to generate the rendering may not be accurate enough for construction
purposes. Most rendering programs hide
unfairness in curved surfaces because they process the surfaces into triangles
and the shading routines smooth the triangles to hide their edges.
This article discusses some of the flexibility you give up
and some of the difficulties you encounter to take advantage of these
benefits. These are the "dirty
little secrets" that most designers learn about only after they buy and
start to use a 3D curve and surface modeling program. This doesn’t mean that you should not use the computer for
design. It means that designers should
know more about the tools they use and understand what restrictions are placed
on them by the program's user interface and what restrictions are placed on
them by the underlying NURB geometry.
Surface Modeling
The field of geometric modeling is huge. Two-dimensional vs. three-dimensional
geometry, wireframe vs. surface vs. solid modeling, relational vs. parametric
vs. variational geometry, parametric vs. implicit equations, the list goes
on. This article, however, will talk
only about smooth curved surface design using NURB (Non-Uniform Rational B-spline)
surfaces, since that is the dominant mathematical technique used by most curve,
surface, and solid design programs, such as Autodesk's Mechanical Designer (all
ACIS modelers), Intergraph's Solid Edge (all Parasolid modelers), and other
independent programs, like New Wave System’s Pilot3D, McNeel’s Rhino3D, and
Think3’s Solid Thinking. If you wish to
transfer exact 3D curve and surface geometry to other CAD programs, you will
have to use NURB surfaces (or a surface type which is mathematically compatible
with NURBs). For example, there are
numerous companies that will take your computer-generated 3D shape and
numerically cut a full-size model out of various materials. These machines are controlled by one of
several surface NC programs like SmartCAM and MasterCAM, using NURB
surfaces. You will have to provide them
with a file containing the NURB surface definition in a standard transfer file
format, such as IGES (Initial Graphics Exchange Specification).
NURBs are the best techniques available for smooth curve and
surface design, but you have to understand their capabilities to get the most
out of your 3D modeling software.
What is a NURB?
NURBs are Non-Uniform, Rational, B-splines. They are equations used to define curves or
surfaces that simulate the designer's batten in terms of stiffness and
continuity. In the early 1970's, 'B' or Basis splines were created (There are
an infinite number of splines.) as a convenient way to define smooth curves and
surfaces interactively on the computer screen.
Rather than have a curve pass through a set of points, like ducks on a
batten, a B-spline creates a curve that is "influenced" by the
positions of defining points called vertices (see Figure 1). The designer changes the shape of the curve
by changing the positions of the defining vertex points. A curve influenced by B-spline vertex points
is smoother than a curve passing through the defining vertex points, but the
curve is by no means automatically fair.
You can create some pretty ugly curves and surfaces with B-splines. In general, all flexible curve and surface
modeling programs need some form of fairing tool.

Figure 1. NURB Curve Showing its Defining Vertex Points and Vertex Polyline
A NURB surface uniquely defines every square inch of a rectangular-like
spline membrane. For editing purposes,
it is usually represented on the screen by drawing a grid of lines on the
surface called rows and columns. Like
the NURB curve, the surface is defined by vertex points that do not lie on the
surface, but are organized as a rectangular matrix or grid of vertex points.

Figure 2. NURB Surface Showing Defining Vertex Points and Vertex Grid or Mesh
To understand and use NURB surfaces effectively, you need to
know what controls you have over their shape: vertices, degree, knots, and weights. Programs might hide this terminology from you, but you need to
know how each of these variables affect the shape of a curve and surface.
For completeness, here is the parametric NURB surface
equation:

P(i,j) Matrix
of vertices: nrows=(k1+1) ncols=(k2+1)
W(i,j) Matrix
of vertex weights: one per vertex point
bi(s) Row-direction
basis or blending polynomial functions of degree M1
bj(t) Column-direction
basis or blending polynomial functions of degree M2
s Parameter
array of row-direction knots
t Parameter
array of column-direction knots
Vertices - The basic shape of a NURB surface is defined
by its rectangular grid of vertex or control points which do not necessarily
lie on the surface. When you move one
of the vertex points, the surface in that local area is pulled in the direction
of the vertex movement as if it was attached to the point by a spring. (see
Figure 3) The surface does not move as
much as the vertex point and the change only affects a small area near the
moved point. The range of influence
depends on the degree of the surface: a
smaller degree (see the next sub-section) means a smaller area of influence and
a larger degree means a larger area of influence. The main drawbacks of these vertices are:
1.
It is more difficult to get the surface to be positioned
exactly where you want.
2.
The vertex mesh hides the shape of the surface.

Figure 3. NURB Curve Example of Moving the Middle Vertex Point
Another approach is to use edit points that lie on the curve
or surface. For every defining vertex
point “floating in space” there is an associated point that lies on the curve
or surface. Some programs allow you to
control the shape of the geometry using these points instead of the vertex
points. The two common ways to
implement shape control using points that lie on the curve or surface are local
control and global control.
Local control using points that lie on the curve or surface means that
when you move a point on the curve or surface, it is mathematically guaranteed
that the change affects the shape only in a small area surrounding that point;
the same as moving one vertex point. (see Figure 4) The problem is that when you move one of the points on the curve
or surface using this technique, some of the surrounding defining points also
move! This technique is the same as
moving a vertex point, except that you are moving the associated point on the
surface.

Figure 4. NURB Curve Example of Points on the Surface - LOCAL
Global curve or surface control means that when you move one
of the defining points on the curve or surface, none of the other surrounding
edit points move. This is called a full
NURB curve or surface interpolation technique.
(see Figure 5) As the selected
defining point moves, the entire curve or surface shape is affected, although
the shape change decreases dramatically as you move away from the changed
point.

Figure 5. NURB Curve Exampe of Points on the Surface - GLOBAL
Although the curve or surface interpolation approach is
global, it gives you the most accurate, direct control over the surface. This
is because you control the shape directly and only the selected defining point
moves. Some feel that this direct,
interpolated control makes it difficult to smooth or fair the curve or
surface. As you will see later, this is
not a problem when you apply dynamic curvature feedback and fine tune shape
control.
Vertices or surface points can be positioned anywhere in
space and are the major shape control factor.
For fairing and detailed shape control, you need to learn more about the
following variables.
Degree - A NURB
curve or surface is represented mathematically by piecewise polynomial blending
functions of the form:
![]()
The highest exponent used in the polynomial (3 in this case)
is the degree of the polynomial. (The
degree is 3 and the order is 4.) NURB
curves use one type of polynomial and NURB surfaces use two different
polynomial types (one for each grid direction - row/column), although most
programs use the same degree for both directions of the surface. The higher the degree of the polynomial, the
more flexibility there is in the curve or surface, but the more uncontrollable
wiggles it might have. Cubic, or degree
3 polynomials are considered to have the best trade-off in flexibility and
stiffness. It is the degree used most
often in CAD programs. Quadratic or
degree 2 curves and surfaces will be stiffer and will be automatically more
fair than cubic curves, but the range of shapes they can achieve will be much
more limited. Many CAD programs fix the
degree to always be 3.
Knots
(Non-Uniform) - NURB curves and
surfaces are polynomials pieced together using knots or a knot vector. Curves use one knot vector and surfaces use
two, one for each grid direction. The
knots define how the polynomial pieces are blended together with the proper
smoothness. Most programs give users
only indirect control over this shape factor.
It is also the cause of many curve and surface shaping and fairing
problems, especially if the surface shape is non-rectangular.
A uniform knot
vector (with constant spacing between the knots) is the most common technique
and works best for most situations. A
program may automatically adjust the spacing of the knots in the knot vector (non-uniform spacing) to account for
uneven spacing of the rows and columns of the surface, but this may not really
help and may cause problems with adjoining surfaces. Some programs also use knots to define tension or knuckle control
over the surface.
The problem with knots is that they have a semi-global
effect on surface shape. If you adjust
the knot spacing in the row direction, then the surface shape is changed for
the full length of the surface, affecting several columns. In addition, if there is a surface attached
to the end of the rows, then it must use the same knot spacing to maintain
exactly the same edge shape. Otherwise,
you have to make sure that the small differences in shape between the two
surface edges are within building tolerances.
This is a major problem with knots. Not only do they have a global affect on the surface, they can
also force changes in adjoining surfaces!
Many programs avoid these problems by fixing the knot spacing to be
uniform for all surfaces. This is a
reasonable solution, but it means that the user should create surfaces with
evenly spaced rows and columns.

Figure 6. Difference Between Uniform (unfair) and Centripetal (smooth) Knot Spacing
The uniform knot spacing works best for evenly-spaced curve
points or evenly-spaced surface rows and columns. If the spacing is not uniform, the alternate knot spacing, like
chord-length or centripetal spacing works best. In figure 6, where the point spacing is un-even, the smoother
curve is defined using centripetal knot spacing. However, non-uniform knot vectors for surfaces can cause bad fit
problems between adjacent surfaces.
This can be a real problem if you expect the surfaces to be transferred
to solid modeling programs without gaps or “leaks”. That is why some programs stick with uniform knot spacing for
NURB surfaces and recommend fairly even spacing for the rows and columns. Actually, nice spacing of the surface
rows and columns should be the goal for all surfaces, no matter how the knots
are spaced. This will make surface
shaping and fairing easier. As long as
you space the curve points and the surface rows and columns fairly evenly, then
you shouldn’t have any problems.
Weights - For
NURB curves and surfaces, each vertex point has an associated weight value that
affects the shape locally near that point.
This weight value is the result of the rational aspect of NURBs, which means that the equation is defined
as a fraction or ratio of
polynomials. The purposes of the
weights are to allow for exact descriptions of conic shapes and to add more
user control over the shape of the surface.
Although each vertex point has its own weight and although each weight
has a local effect on the surface, a change in a vertex weight (1.0 is the
default weight) does not necessarily change the surface the way you want. In practice, changing a vertex weight value
can cause more problems for curve or surface fairing. The best approach is to apply weight changes only near the end of
the design process to achieve very specific local effects. Do not use weight control to create
shapes that can be achieved by moving vertex points. Some CAD programs severely limit the user’s
control over weight values because of these problems. Most curve and surface shapes can be defined and faired without
changing the weight values.

Figure 7. Difference in Curve Shape Due to Weight Change
In figure 7, the weight factor of the middle point was
changed from 1 to 10. No other changes
were made to the vertex positions, the degree of the curve, or the knot vector
definition. Note how the weight change
flattens the curve on either side of the middle point and how it leaves a
little curve “lump” right at the ends of the curve. Even though a weight change has a (somewhat) local effect, it
tends to create unwanted flats and bumps.
Now that you have been introduced to the NURB shape controls
(vertices, degree, knots, and weights), the next section will discuss many of the
3D surface design problems that you may encounter and some of their solutions.
Some of the more insightful readers might note that if a
program uses uniform knot spacing and fixes the weights to 1.0, then this would
be a simple uniform B-spline curve or surface.
Then why does a 3D modeling program use NURBS? That is a good question and I can make a strong argument that
NURBs are not necessary, even for conic shapes. I guess the reason is that NURBs form a superset of many
different spline techniques and that if you wish to transfer surface geometry
between programs, then it is a good solution.
While we’re at it, I might even say that NURB surfaces,
because of their rectangular nature and the difficulty in smoothly connecting
them together into complicated topologies, are seriously flawed. That is why there is so much interest lately
in subdivision surfaces. These surfaces
allow for very complicated topologies, like 3D polygon structures. Some subdivision techniques even incorporate
C2 continuity or smoothness constraints.
So far, however, subdivision techniques have only become popular for
organic shapes that don’t have the same precision or smoothness needs as
manufactured parts.
Dirty
Little Secrets
These are some of problems you can expect to encounter when
using one of the NURB surface design programs.
Rectangular Shape Spline Mesh
The NURB surface is a rectangular mesh of rows and columns
with four hard corner points. The
entire surface is continuous, except for these four points. You can stretch and distort the surface to
any shape by repositioning the vertex points, but the more non-rectangular of a
shape you make, the more difficult it will be to fair. It is the designer’s job to determine how to
break down a full 3D model into a collection of rectangular-like pieces, how to
deal with the four hard corner points, and how to maintain the proper
continuity between surfaces. There is
no one way of doing this.
For example, a full keel, wineglass shaped, sailboat hull is
typical of one of the more difficult shapes to define. The hull is not rectangular and is difficult
to model with one surface. Figure 8
shows how the J Boat Endeavor I was modeled by one NURB surface because the aft
end of the keel made a smooth transition up to the transom. Even so, there are many subtle shape
problems (bumps and wiggles) that have to be dealt with due to the extreme
distortion of the one rectangular surface.

Figure 8. J Boat Endeavor I Modeled With One NURB Surface


Figure 9. Front and 3D View of One Non-Rectangular Surface
Figure 9 shows another example of one surface distorted into
a very non-rectangular shape. It also
shows the rows and columns of the surface and shows a number of planar contours
of the surface. You can distort
the NURB surface with good results, but I would look at the surface a little
bit more where the contours change from a ‘V’ shape to a ‘U’ shape. This might indicate an area where the shape
might not behave the way you want.
Be careful, however, since shallow planar cuts of surfaces
always magnify surface unfairness. A
change in the surface by less than the building tolerance might have a dramatic
effect on the shape of these planar cuts.
In the old days, when draftsmen had to draw the three different views of
a surface by hand, they had to both fair the curves and to match up the
dimensions in the three views. It is
very difficult to do both at the same time.
If they erred a little bit, it was always in the direction of making the
curves look smooth and fair. If you
measured and compared distances in the three views, you could always find small
errors. (hopefully within building tolerances!) With modern NURB surface design programs, it is the other way
around. The programs guarantee that all
three views match up exactly and that all planar cuts are calculated or derived
from the shape of the surface. This
means that it will be difficult at times to make all of the planar surface cuts
look perfectly fair, especially for very shallow surface cuts. Fair only to within building
tolerances. It may be irritating to
look at some of these curves, but you will drive yourself crazy trying to get
them perfect.
Finally, if there are more than 4 distinct, hard points on a
continuous, smooth surface, then you will probably have to break it into two or
more connected surfaces and try to maintain curvature continuity.
Clutter of Vertex Mesh and Surface Shape
Since the defining vertex points do not lie on the NURB
surface, most programs allow you to connect the vertices with straight lines to
make them more visible. This grid of
straight lines is often called a vertex mesh.
If you do not connect the vertices with a mesh, then the vertices are
floating in space and it becomes very difficult to know which part of the
surface they influence, especially in certain views. If you display the vertex mesh, however, it clutters up the
screen and hides the shape of the surface.
For detailed surface shaping with many rows and columns, this is a real
problem. (See Figure 10)
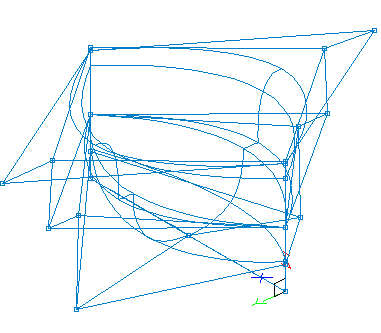
Figure 10. 3D View of Multiple Surfaces Showing Clutter of Vertex Lines
To avoid this problem, some programs use points that lie on
the surface. This cleans up the clutter
and makes the surfaces easier to see and manipulate. (See Figures 11 and 12)
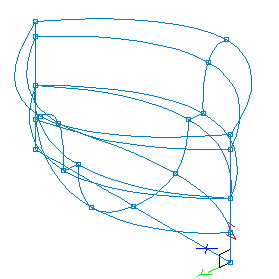
Figure 11. Same 3D View Showing On-Surface Edit Points

Figure 12. End View Showing Edit Points on the Surfaces
Planar Surface Cuts Cannot be Controlled Directly
NURB surfaces are defined using a grid of row and column
vertex points that can be moved anywhere.
You cannot directly grab and alter the shape of any traditional planar
line cut of the surface. These lines
are considered to be derived lines or surface cuts which can be automatically
calculated from the surface definition.
Some programs, however allow you to display these lines while dragging a
control point so that you can immediately see what happens when a vertex point
is moved. To change the shape of a
planar cut, for example, you have to move the vertex point that lies closest to
the point on the cut you wish to change.
This design by rows and columns is the biggest adjustment required by
the experienced hand draftsmen.
Adding and Deleting Rows and Columns
One can start with a very simple NURB surface consisting of
two rows and two columns, and then add in additional rows and columns to
increase the flexibility and control of the surface. In doing so, the program must add the row or column in over the
entire length or width of the surface.
There is no allowance for partial rows or columns. This means that if you want to add rows and
columns near one end of a surface to define some local detail, then these rows
and columns must extend over the entire length and width of the surface, whether
you want them to or not. Remember
that the only way to add shape control is by adding in control vertices, and
the only way to add in control vertices is by adding them in as a complete row
or column.
Spacing of Rows and Columns
The smoothest surface shape depends on a relatively even
spacing of the rows and columns. If
there is more than a 2 to 1 ratio of consecutive row or column spacing, you
will begin to see some very strange anomalies, such as hard bumps and loops. A program could adjust the knot vector to
minimize the bumps and loops of uneven spacing, but this adjustment can cause
other difficulties. For example, if two
surfaces are to be joined exactly, edge-to-edge, then the two surfaces must
have the exact same knot vector at that edge.
If you have several surfaces attached together with common edges (a
polysurface), then a change in the knot vector in one surface can affect the
shape of all of the connected surfaces.
One technique in dealing with attached surfaces is to use uniform knot
spacing for all surfaces and always add in rows or columns by splitting the
difference between two existing rows or columns. This will always maintain a reasonable 2 to 1 ratio in row and
column spacing acceptable for uniform spacing.

Figure 13. Uneven Spacing of Columns

Figure 14. Added Column to Create Even Spacing
Piecing Together Surfaces
Rarely can you use one NURB surface to define a whole
object. If two surfaces meet edge to
edge, you need to understand the requirements of attaching two surfaces
together. There are two types of
attachment: exact and approximate.
To form an exact attachment between two surfaces, the two surfaces must
match up exactly along their entire length.
The common surface edges must have the exact same edge vertex points,
they must use the exact same polynomial degree at the edge, they must use the
exact same knot vector at the edge, and they must use the exact same weight
values at the edge. Otherwise, the
mathematical definition and therefore, the shape of each surface at the edge
will be different. If the two surfaces
do not agree exactly at the common edge, then the attachment is considered to
be approximate. It is then up to the user
to manually make sure that the two approximate edges are within building tolerances
of each other. If two surfaces match
exactly and the user adds a column that runs into the attached surface, then
the program must add a column to the attached surface or the two surfaces will
not be joined exactly anymore.
Matching up Existing Designs
The original goal of B-splines was to create smooth curves
and surfaces interactively on the computer screen. That is why they use vertices that do not lie on the curve or
surface. But these floating vertices
make it difficult to recreate shapes that currently exist. For example, if you have a set of
measurement points (perhaps from a 3D digitizer) and wish to create a NURB
surface representation of that shape, you will have difficulty trying to position
the vertices to achieve that shape. Some
programs allow you to digitize the sections of an existing object and to use
that as an interactive guide for moving NURB surface vertex points. You move the vertex points until the surface
section shape matches the digitized section shape. This is a very tedious process.
A better approach is to automatically fit the NURB surfaces to the input
data or the digitized sections so that the surface passes through the
measurement points. You will still have
to perform the final shaping and fairing, but the matching-up time will be
greatly reduced.
For those interested in scanning in a 2D set of curves that
define a 3D object, there is still quite a bit of work left to do. First, the scanner reads the whole drawing
as a rectangular grid of dots (a bitmap).
It doesn’t know anything about curves at this point – just dots. To convert the dots into curves, you can use
one of two methods. The first is to use a raster to vector converter program to
connect the dots to form polylines (not curves). Unfortunately, if the original curves overlapped each other or
crossed each other, the raster to vector converter will not do a good job of
creating one simple polyline entity per curve on the drawing. You will have to import the raw vector
polylines into a CAD program and clean them up yourself. This could take some time. The other technique is to find a CAD program
that can read the raw, scanned bitmap and display it on the screen. You would then define polylines or curves
that overlay the bitmap curve images on the screen. People are better at raster to vector conversion than
programs. Either way, however, you will
have to spend some time getting the curves ready for skinning or lofting.
Rather than scanning a 2D drawing, you could use a digitizer
tablet with a cross-hair puck or stylus.
You would tape the drawing to the tablet and use a program to trace in
each curve. This also takes time to set
up the coordinate system and to trace in each curve. It is probably easier and faster to display the scanned bit map
on the screen and to “digitize” the image on the screen. [Watch out for screen
distortion of the bitmap.] A lot will
depend on what devices and software you have.
If you expect to do a lot of this “reverse engineering”, then it
probably pays to research the different devices and software available to do
the job.
In all cases, there is no free lunch. What you are trying to do is to go from less
information (point or curve data) to a NURB surface definition, which is a
complete, exact definition of the surface.
There are an infinite number of solutions to this problem. It requires both software to do the surface
fitting and a human to judge the results.
The quality of the results depend on the amount of input shape data you
have, the accuracy of the data, the organization of the data (curves, point
cloud of data, etc.), and the ability of the software to organize and use this
data. For more information about this
subject, see the article on Reverse Engineering.
Detailed Surface Shaping
In the old, hand drafting days, you had many tools to create
curved shapes: French curves, ship’s curves, templates, battens and ducks, and
even freehand sketching. For designing
one curve, you might use several, different curve templates. In addition, you might also have a number of
battens of different lengths and flexibilities. Using a surface design program, you just have one tool: a NURB
surface. A NURB surface is quite adaptable,
but it really isn’t as flexible as the collection of original hand drafting
tools. That is why it is very important
for a surface design program to give users detailed shape control tools.
Some programs have difficulty with detailed surface
shaping. They might have many ways to
generate surfaces using lofting, extrusion, and sweeping commands, but few
commands to control the resultant shape.
There is no guarantee that if the shape and path curves of a sweep
operation are perfectly fair, the resultant surface will be fair. Even if the surface is fair, you may still
want to manipulate the resultant shape.
This requires commands that allow you to move and fair the individual
surface edit points. Surface
evaluators, like Gaussian curvature are not the answer because the surface
curvature cannot be displayed dynamically while you are moving the surface edit
points. You also need some sort of fine
tune shape control. Otherwise, you will have to zoom in very close to the edit
point to get the resolution you need for detailed shaping. When you zoom in that close, however, you
lose all sense of what you are shaping.
Some programs provide automatic fairing or smoothing tools,
such as a command that equally respaces all of the points on a surface. This eliminates problems associated with the
knot vectors and the uneven spacing of defining points. The resultant surface will be smoother, but
it probably won’t be the shape you want.
In old hand drafting days, designers were always told not to let the
curves or batten define the shape of the object. Today, you must not let the 3D modeling “curves” or the program
define the shape of the object. The
joke nowadays is to ask who designed the shape of an object, the designer or
the computer program. [i.e. Is that really
the shape you wanted, or did you just give up?]
For complete control over your surfaces, you need detailed
surface shaping tools. You need a way
to eliminate the clutter of the vertex mesh, you need some form of dynamic
curvature fairing feedback or display, and some sort of fine tune edit point
move command.
Fairing and Smoothing Surfaces
In
spite of what you may have heard, there is no mathematical definition of
fairness. This does not mean that
everyone would disagree on the fairness of a curve or that there are no
mathematical tools to use to check for bumps and wiggles. It just means that there are no good ways to
automatically fair a curve or surface by computer without some form of human
input.
For example, one of the tricks in fairing a manual
spline is to lift certain ducks for a moment to “relax” the batten. This smooths the curve, but it doesn’t
necessarily maintain the shape that you want.
With the computer, you have the same problem of getting the shape you
want and making sure that the shape is fair.
Automatic computer fairing techniques may smooth a surface, but they do
not have the human judgment to make this shape vs. fairness trade-off.
Some programs say they guarantee fairness of a curve or
surface, but this is only an opinion and is usually done by severely limiting
the shape of the surface. For example,
if someone gave you a batten and three ducks, it would be impossible to create
a curve that was not considered to be fair.
On the other hand, you would be severely limited in the range of shapes
you could draw.
Most surface design and fairing programs provide ways to
check the fairness of a surface by using some form of second derivative or
curvature curve, or by using some form of surface curvature color mapping. Designers don’t need to know the mathematics
behind these techniques. They just need
to see how the technique magnifies all bumps, wiggles, and inflection
points. Hopefully, the curvature
information is displayed in real time while the user edits the shape of the
surface. The designer interactively
changes the shape of the surface to obtain a smooth derivative or curvature
curve. As you can see, the designer is
actively involved with the fairing process.

Figure 15. NURB Surface Curve With Unfair Overlaid Curvature Curve
Note that the points where the orange curvature curve
crosses the surface curve are inflection points on the curve. The goal of fairing is to move the defining
curve edit points to make the curvature curve smooth. If you make the curvature curve smooth, then the underlying curve
is very smooth.

Figure 16. NURB Surface Curve With Faired Overlaid Curvature Curve
The top surface curve in figure 16 was faired to within .002
units over a length of 15.0 units. This
means that the user can accurately see changes in the curvature curve when the
surface curve is moved by 0.002 units.
To do this, the program must provide some form of fine tune shape
control without having to zoom in on a portion of the screen. For details of this specific fairing
process, see the tutorial on fairing NURB curves and surfaces.
The problem with fairing NURBs is that the surfaces are so
sensitive to the knot values. If a
program uses uniform knot spacing, then the NURB surfaces need to have fairly
evenly spaced rows and columns. When
the knot spacing does not match the spacing of the rows and columns, you may
have fairing problems. When a NURB
surface is stretched into a very non-rectangular shape, even non-uniformly
spaced knots do not help. In addition,
non-uniform knots cause other problems, as mentioned before.
Another problem is that you cannot control the shape of the
planar cut lines directly. You can only
change the shape of the rows and columns of the surface. This means that it will be difficult in some
cases to make shallow planar cuts of surfaces look just right. The slightest change in the shape of the
surface will cause a noticeable change in the shape of the planar cut
line. During the fairing process, you
must fair only to within the building tolerance and not worry too much about
how perfect the planar lines cuts look.
Vertex Weight Values
Although weights have a local influence on the shape of the
surface, manipulating their values can be difficult. A common approach is to try to obtain the desired surface shape
by only adding and manipulating rows and columns of vertices. After you have roughed out the surface
shape, you can then change the weight values to achieve specific local
effects. Most objects, however, can be
defined without changing the vertex weight values. Only experienced users should try manipulating these values.
Relational vs. Trimmed Surfaces
There has been some discussion between two ways of attaching
or connecting surfaces: trimmed
surfaces vs. relational or attached surfaces.
For trimmed surfaces, one surface is pushed through another and the
program automatically trims off the overlap.
An example of this is to push the root end of a wing through the side of
an airplane fuselage. For relational or
attached surfaces, the root edge of the wing surface is attached to the
fuselage surface of the airplane. If
the wing surface shape is changed, it will always stay attached to the fuselage
surface, and if the fuselage surface changes shape, the end of the wing will
stay attached.
The obvious advantage of attaching one surface to another is
that you do not have to worry about whether the surfaces intersect if one or
the other surface changes shape. The
downside is that if the attached-to surface changes shape, then the attached
surface changes shape. For the wing and
fuselage surface attachment example, if the fuselage surface changes shape near
the wing, then the attached wing surface changes shape! For airfoil-shaped wings, you do not want a
change in fuselage shape to change the shape of the airfoil. For trimmed surfaces, you would just have to
make sure that the wing root end penetrates the side of the fuselage surface by
a little bit. The shape of the wing is
independent of the shape of the fuselage.
You can “pick up” the wing, shift its position, and re-penetrate the
fuselage without changing its shape.
There are benefits and disadvantages to both
approaches. Attachment or relational
geometry works best when the two surfaces or geometry shapes relate and are
dependent on one another, such as when you attach a structural rib to the side
of a surface. Trimmed surfaces work
best when the two surfaces must be joined, but their shapes are independent of
each other. Trimmed NURB surfaces also
work best if you need to convert the surface model to industry standard solid
modelers. Relational attaching of one
surface to another can leave very small gaps between the surfaces that are very
difficult to deal with in solid modelers.
Calculations
Most of the specialized surface design programs use or allow
open surface design geometry. This
means that the programs do not requires a complete, closed solid geometry at
all times. Solid modeling has some
advantages when it comes to calculations, but it makes the process of modeling
surface geometry much more difficult, especially in the initial concept design
phase. This means that the surface
design software has to do a lot of work to calculate the volumetric properties
of an open surface model.
The first step is to cut all of the surfaces at a series of
cross-section positions along the length of the object. The next step is to somehow combine these
surface cuts into realistic, trimmed and closed cross-section shapes. This can be very difficult for intersecting
and open surfaces, and for surfaces that do not quite match up exactly along
common edges. Finally, some form of
longitudinal integration can be performed to produce the final results. For all of these programs, the key to
obtaining accurate results is to verify the shapes of the cross-section cuts
before the calculations are done. If
the cuts look good (and you have enough of them covering the length of the
model), then the results should be accurate.
Be aware that many problems can arise during the cross-section cutting
and reconstruction phase.
To avoid this problem, the program could require that you
always create a closed and trimmed surface model before the calculations are
done. Then the program could
triangularize the model and use solid modeling volume calculations
techniques. The downside to this method
is that it can be difficult to create the surfaces to close the object. This can be quite a distraction during the
early stages of modeling an object.

Figure 17. Automatically Trimmed and Closed Cross-Sections Used For Volume Calculations

Figure 18. 3D View of Cross-Sections Used For Volume Calculations
Conclusion
NURBs are the dominant mathematical technique used for
designing curves and surfaces of manufactured objects. In spite of this, there are many things you
need to know to get the most out of your surface design or CAD program. This article discussed many of these hidden
problems. Since all NURB-based programs
vary greatly, the best advice is to get the demos of all of the surface design
programs and spend some time with them trying to design various objects. The user interface of a program can have as
much of an impact on your ability to get the job done as which mathematical
technique is used to define the object.
Don’t wait until after you buy the program to learn the truth.